Background

单缝衍射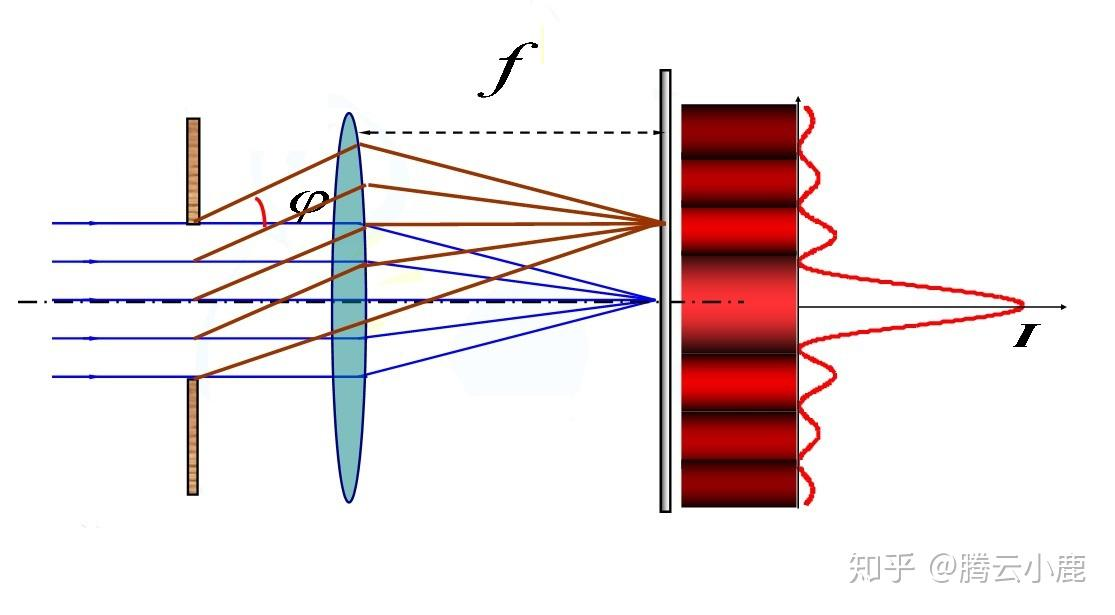
image.png

双缝干涉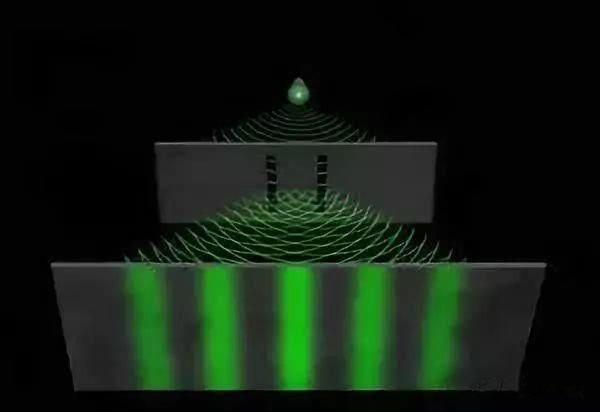
image.png
大抵是高中背了一次，大学物理又背了一次，帮同学写小作业拾起来再复习了一次

单缝衍射

单缝衍射是光在传播过程中遇到障碍物，光波会绕过障碍物继续传播的一种现象。如果波长与缝、孔或障碍物尺寸相当或者更大时，衍射现象最明显。依据光源、衍射屏（障碍物）及接收屏相对位置的不同，常将衍射分为两类，即菲涅尔衍射与夫琅和费衍射。在光学里,菲涅耳衍射(Fresneldiffraction)指的是光波在近场区域的衍射,即光源或衍射的图样的屏与衍射孔(障碍物)的距离是有限的。菲涅耳衍射积分式可以用来计算光波在近场区域的传播,因法国物理学者奥古斯丁·菲涅耳而命名,是基尔霍夫衍射公式的近似 光源和光屏到障碍物的距离均不是很远，并且没有使用透镜。此时光线不是平行光，即波阵面不是平面。这种情况是菲涅尔最早（1818年）描述的，所以称为菲涅尔衍射。
光源和光屏到障碍物的距离都很大，此时入射光为平行光，波面是平面，衍射光也是平行光。这种衍射称为夫琅禾费衍射。在实验室里，我们可以很容易的用透镜使入射球面光波变成平行光，很容易实现夫琅禾费衍射的条件。显然，菲涅尔衍射是普遍情况，夫琅禾费衍射只是它的特例。

双缝干涉

在量子力学里，双缝实验，或称双狭缝实验（英语：Double-slit experiment）是一种展示光子或电子等微观物体的波动性与粒子性的实验。双缝实验是一种“双路径实验”。在双路径实验里，微观物体可以同时通过两条路径或通过其中任意一条路径，从初始点抵达最终点。这两条路径的程差促使描述微观物体物理行为的量子态发生相移，因此产生干涉现象。另一种常见的双路径实验是马赫-曾德尔干涉仪实验。

双缝实验的基本仪器设置很简单，如图所示，将像激光一类的相干光束照射到一块刻有两条狭缝的不透明板，通过狭缝的光束会抵达照相胶片或某种探测屏，从记录于照相胶片或某种探测屏的辐照度数据，可以分析光的物理性质。光的波动性使得通过两条狭缝的光束互相干涉，形成了显示于探测屏的明亮条纹和暗淡条纹相间的图样，明亮条纹是相长干涉区域，暗淡条纹是相消干涉区域，这就是双缝实验著名的干涉图样。

在经典力学里，双缝实验又称为“杨氏双缝实验”，或“杨氏实验”、“杨氏双狭缝干涉实验”，专门演示光波的干涉行为，是因物理学者托马斯·杨而命名。假若光束是以粒子的形式从光源移动至探测屏，抵达探测屏任意位置的粒子数目，应该等于之前通过左狭缝的粒子数量与之前通过右狭缝的粒子数量的总和。根据定域性原理（principle of locality），关闭左狭缝不应该影响粒子通过右狭缝的行为，反之亦然，因此，在探测屏的任意位置，两条狭缝都不关闭的辐照度应该等于只关闭左狭缝后的辐照度与只关闭右狭缝后的辐照度的总和。但是，当两条狭缝都不关闭时，结果并不是这样，探测屏的某些区域会比较明亮，某些区域会比较暗淡，这种图样只能用光波动说的相长干涉和相消干涉来解释，而不是用光微粒说的简单数量相加法。

双缝实验也可以用来检试像中子、原子等微观物体的物理行为，虽然使用的仪器不同，但仍旧会得到类似的结果。每一个单独微观物体都离散地撞击到探测屏，撞击位置无法被预测，演示出整个过程的概率性，累积很多撞击事件后，总体又显示出干涉图样，演示微观物体的波动性。

实验

基于python的光学仿真包含了单缝衍射和双缝干涉两个部分，本光学仿真主要基于包含夹角、距离的光强公式，是一个TOY EXAMPLE，可以认为是知道理论和公式来计算图像，不过仿真大抵如此，而且完全符合公式以及图像。

单缝衍射：

参数设定：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# param:
# I0:初始光强
# a: 缝宽
# λ:波长
# f:透镜到光屏距离
# w*h:光屏大小
# d:采样间隔
  
I0=255
a=0.1*10**-3
λ=300*10**(-9)
f=1
w=h=0.05
d=0.0001

# 中间量：
# α：角度
# θ: 高度到光心倾角

光屏大小的图片矩阵来记录对应的光强：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np
image=np.zeros((int(w//d),int(h//d)))

for i in range(image.shape[0]):

    for j in range(image.shape[1]):
        x=np.abs((image.shape[0]//2-i))*d
        # y=j-image.shape[1]//2
        θ=np.arctan(x/f)
        α=np.pi*a*np.sin(θ)/λ

        if α!=0:
            image[i,j]=I0*(np.sin(α)/α)**2
        else:
            image[i,j]=I0

w1,h1=image.shape
#(500, 500)

图片展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import matplotlib.pyplot as plt
from matplotlib import cm
# 支持中文
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题

plt.title("全局图片")
plt.imshow(image)
plt.ylabel("y(%.1f mm)"%(d*1000))
plt.colorbar()
plt.show()


plt.title("局部放大强度图（强度着色）")
plt.imshow(image[w1//4:w1*3//4,h1//4:h1*3//4])
plt.colorbar()
plt.show()

plt.title("局部放大强度图（黑白未着色）")
plt.imshow(image[w1//4:w1*3//4,h1//4:h1*3//4],cmap='gray')
plt.colorbar()
plt.show()

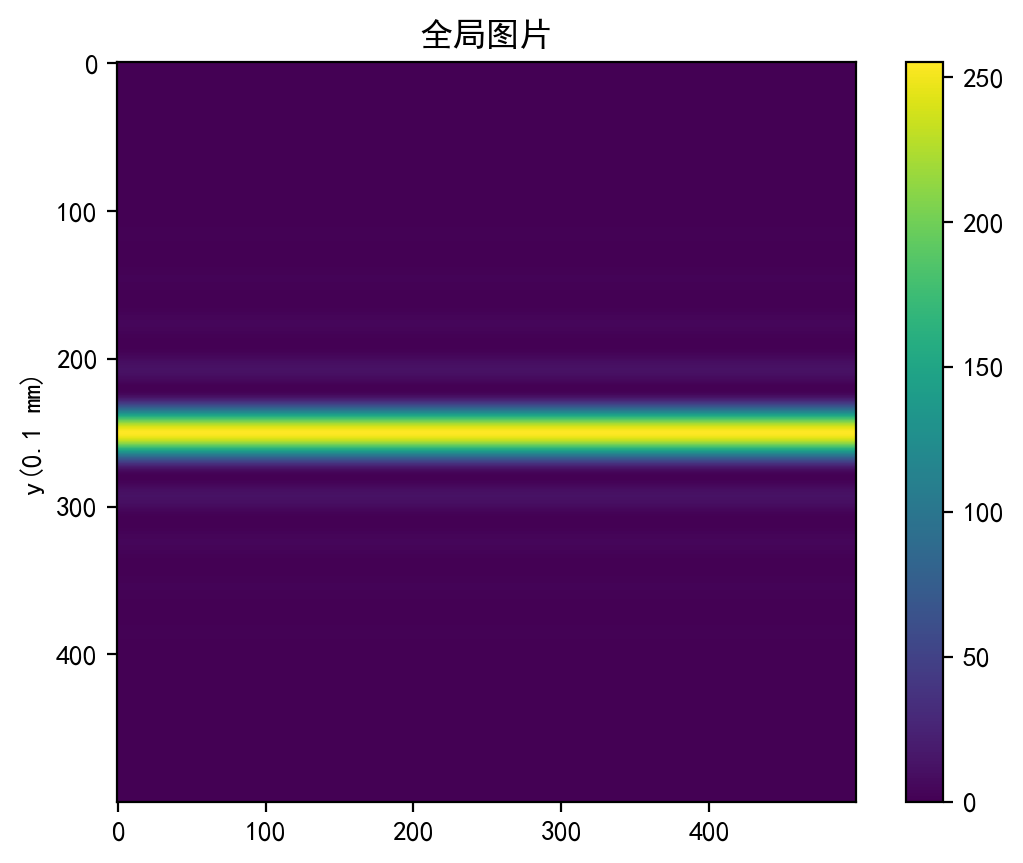
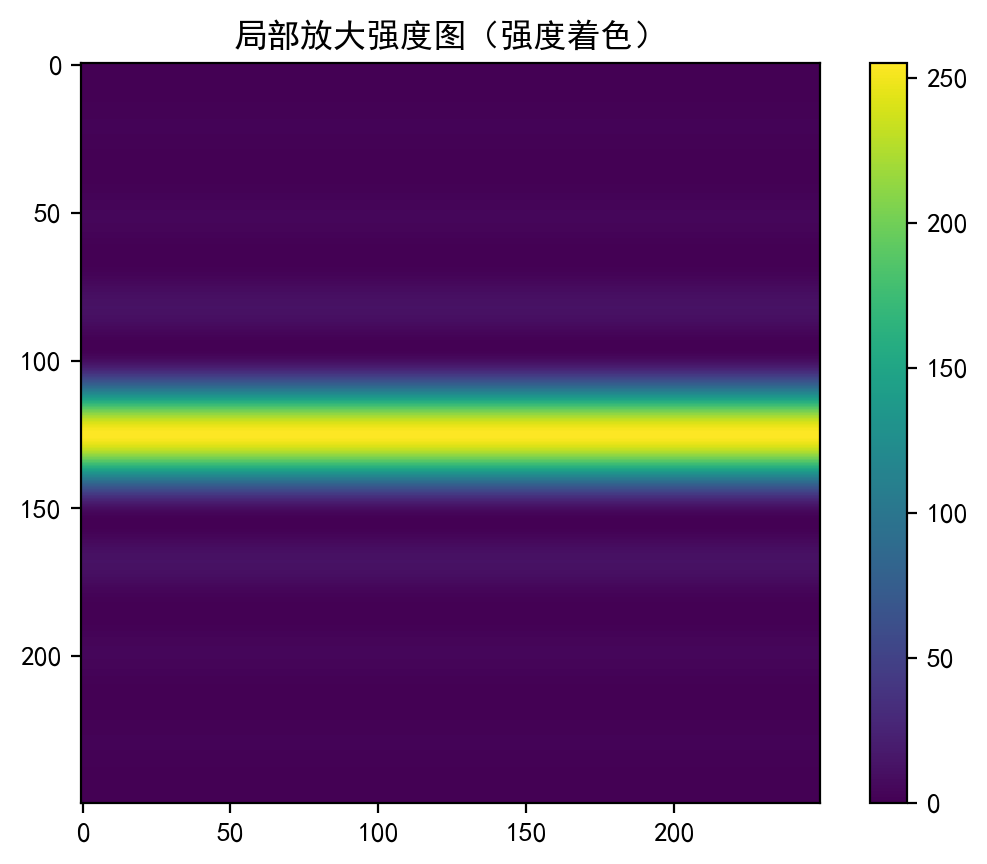
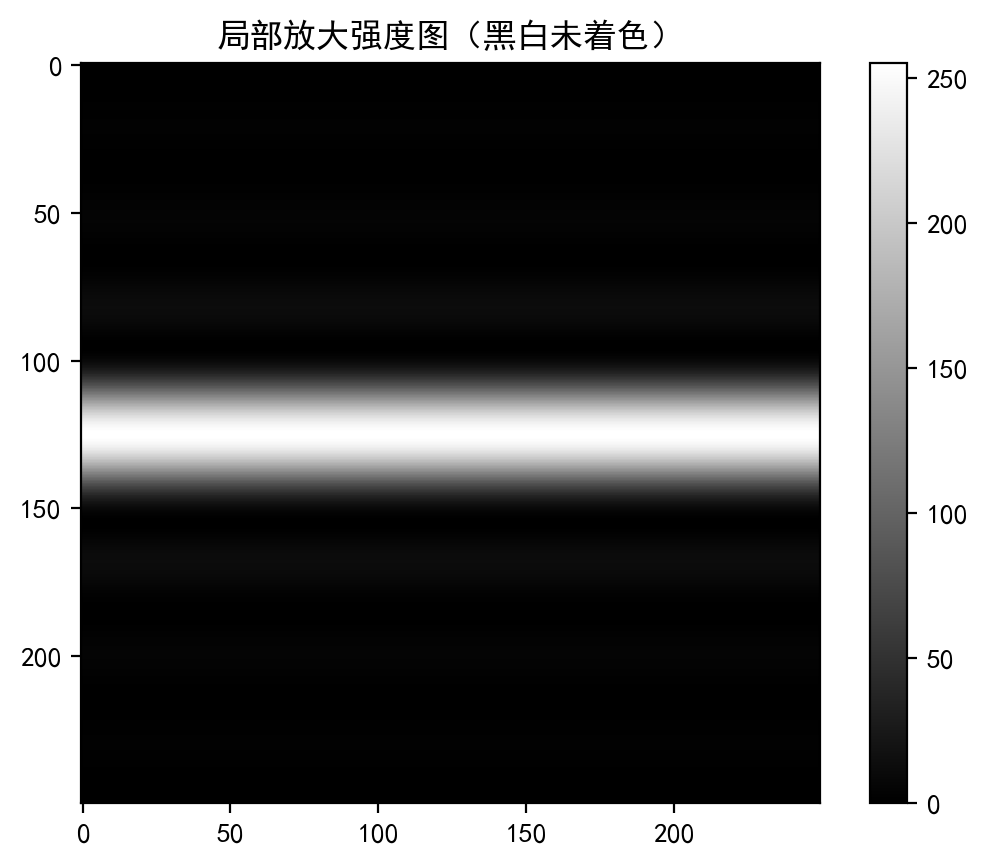
image.png
image.png

image.png

双缝干涉

参数:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
# 参数:

# 缝间隔
d=0.25*10**(-3)
# 双缝到屏的距离
D=1
#波长
λ=500*10**(-9)
#原光强
I0=10
#光屏大小：限制计算复杂度,和展示图像的细密程度
w=h=0.04
#采样间隔
s=0.25*10**(-3)

S1=(d/2,0)

S2=(-d/2,0)

O=(0,D)

由于对称性，完全可以进行优化，即只与一个坐标有关

1
2
3
4
5
#在高度x介于(0,h/2)采样，采样间隔可设置
sample_times=int(h/s)+1
# x轴采样值
X=np.linspace(0,h/2,sample_times)
print("单向采样次数%d,采样间隔为%2f"%(sample_times,s))

光强计算

1
2
3
4
5
6
7
8
9
Il=[]
for i in X:
    P=(i,D)
    PS1=((i-d/2)**2+D**2)**0.5
    PS2=((i+d/2)**2+D**2)**0.5
    dL=PS2-PS1
    I=2*I0*(1+np.cos(2*np.pi*dL/λ))
    Il.append(I)
Il=np.asarray(Il)

光屏展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np

# 支持中文
plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题
plt.rcParams['savefig.dpi'] = 200 #图片像素
plt.rcParams['figure.dpi'] = 200 #分辨率

# step2 设置绘图样式，这一模块的扩展参考第五章进一步学习，这一步不是必须的，样式也可以在绘制图像是进行设置
mpl.rc('lines', linewidth=2, linestyle='-')
# step3 定义布局
fig, ax = plt.subplots()
# step4 绘制图像
# step5 定义绘图样式
ax.plot(X,Il, label='光强') 
# 先将显示的坐标图的上边框和右边框去掉，即设置它们的显示方式为不显示
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
# 将坐标图的下边框和左边框作为坐标系的x轴和y轴，并调整坐标轴的位置
ax.spines['bottom'].set_position(('data',0))  #data表示通过值来设置x轴的位置，将x轴绑定在y=0的位置
ax.spines['left'].set_position(('axes',0.0))  #axes表示以百分比的形式设置轴的位置，即将y轴绑定在x轴50%的位置，也就是x轴的中点
# step5 添加标签，文字和图例，这一模块的扩展参考第四章进一步学习
ax.set_xlabel('X')
ax.set_ylabel('光强')
ax.set_title("光强随x变化(单向)")
ax.legend()
plt.show()

光屏像素点数

1
2
3
4
5
Il_2=np.hstack((Il[::-1],Il))
Il_3=np.tile(Il_2,(sample_times*2,1))
Il_3=Il_3.T
Il_3.shape
#(322, 322)

光强彩色图渲染

1
2
plt.axis('off')
plt.imshow(Il_3[:,:])

image.png

灰度图展示

1
plt.imshow(Il_3[:,:],cmap='gray')

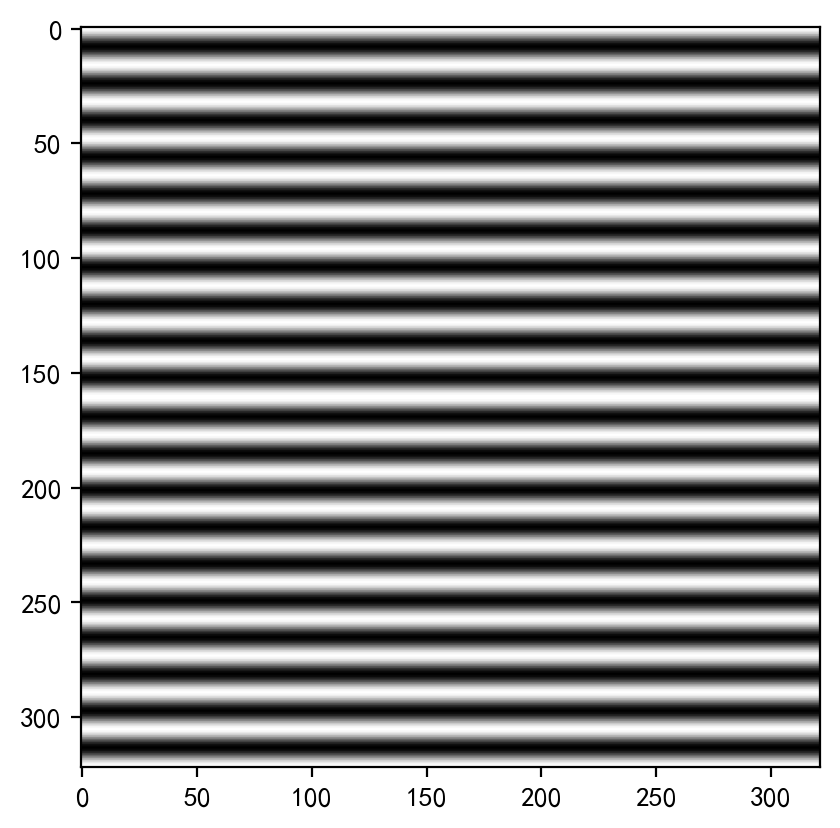
image.png
总觉得哪里不太对劲，可能还需要哪里有些问题，对了plt.axis(‘off’)可以关闭坐标轴

1
2
3
4
5
6
7
# # # remap to 0-255

# Il_3*=255/Il_3.max()

# # plt.imshow(Il_3[:,:],cmap='gray')

# plt.imshow(Il_3[:,:])