Kolmogorv-Arnold网络是MLP的promising替代方案。

  • KAN的激活函数在边上，而与之相对的是，MLP激活函数在节点上。
  • 可训练的激活函数
    这一简单的变化使KAN在准确性和可解释性方面都优于MLP。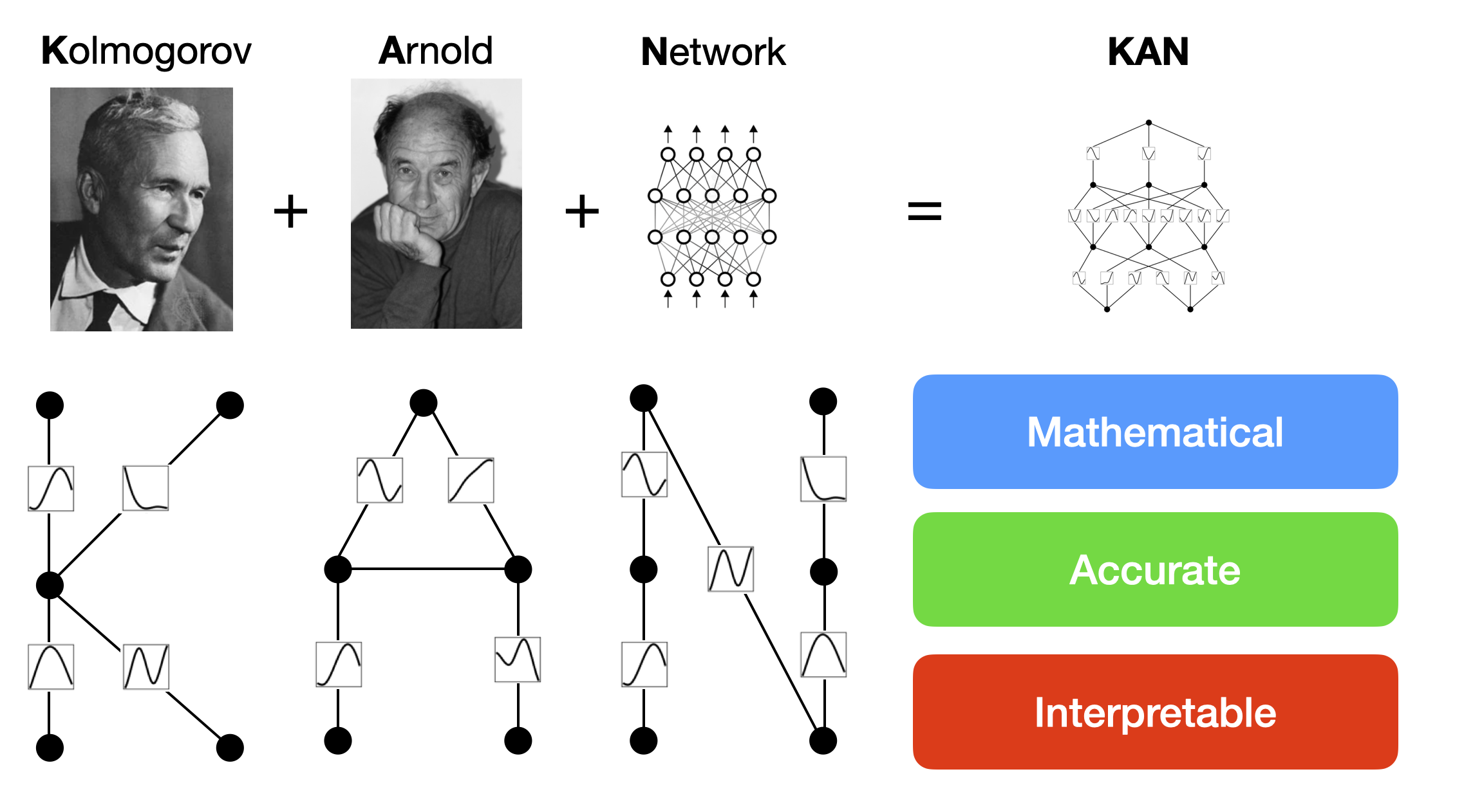
    image.png

链接

arxiv论文
KAN 官方python库文档
有一说一，这个论文和文档写得非常有反映研究思路，比较渐进性和基础。

论文阅读

before reading

I’m concerned about its performance, training methods and all kinds of tradeoff.

reading

本文提出了一种名为Kolmogorov-Arnold Networks（KANs）的新神经网络架构，它受到Kolmogorov-Arnold表示定理的启发，是多层感知机（MLPs）有前景的替代方案。

要点

  1. KANs与MLPs的区别：传统的MLPs在节点（或称为“神经元”）上使用固定的激活函数。而KANs在边上（或称为“权重”）使用可学习的激活函数。

  2. KANs的特点：KANs中完全没有线性权重。每个权重参数都被一个参数化为样条的单变量函数所替代。

  3. 优势：准确性和可解释性

    • 准确性：实验表明，KANs在数据拟合和偏微分方程（PDE）求解方面，能以较小的网络规模达到或超过较大MLPs的准确度。从理论和经验上，KANs的神经缩放定律都比MLPs更快（能用较小参数实现较好性能）。
    • 可解释性：KANs可以直观地可视化，并且容易与人类用户交互。这使得KANs成为科学家（重新）发现数学和物理定律的有力工具（得益于局部样条曲线的易于可视化）。

对比MLP和KAN

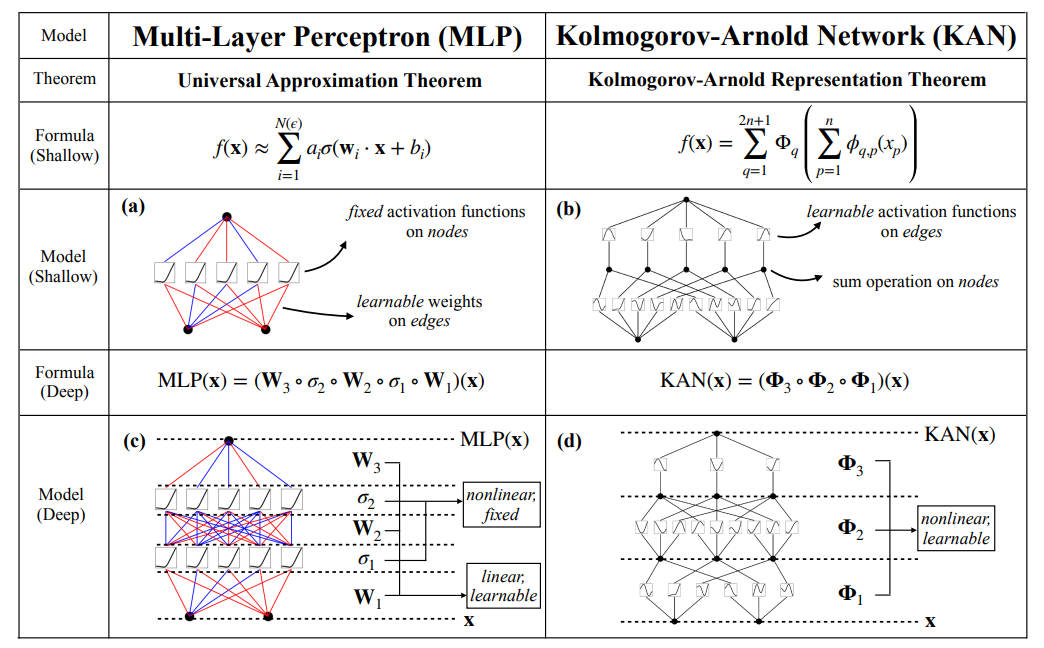
image.png

MLP，即全连接前馈神经网络，是用于非线性函数近似的默认通用模型，其理论依据是通用近似定理。但MLP不是最佳的非线性回归器，而且有很多缺点，比如在transformers中MLP占据了大多数非embedding（文本嵌入编码）用的参数，并且解释性差，没有后续分析工具。
MLP在节点（神经元）上使用激活函数，KANS在边（权重）使用可学习的激活函数，KANs没有线性参数矩阵W，而是把每个参数wij换成了参数化为样条曲线的1D函数，形成了函数矩阵。KANs的节点仅仅进行对函数矩阵运算后的结果进行求和。KAN可能成本高，每个权重都换成了样条函数，然而，KAN的计算图比MLP小很多，对于偏微分方程PDE求解问题，两层宽度为10的KAN比4层100宽的MLP精度更高，并且节省了100倍的参数（这样的比较是否有点不公平，10-4已经很低了，为了过低的损失没必要，参数也不是直接省的，而是从堆叠宽深变成了样条参数）

image.png
激活函数是基函数+样条函数，其中，基函数是Silu函数，样条函数是样条函数线性组合，可训练参数只有样条函数组合系数c，w是一个乘数因子用于控制尺度
初始化：w使用Xavier，样条函数初始化为接近0，即spline(x) ≈ 0，通过c使用（0,sigma^2）正态分布采样实现，sigma=0.1

实验：没有在ML常见任务上比较：minist图像任务、NLP、tabular任务

而是主要在符号回归，包括toy数据集、费曼数据集，外加一个节理论实验

KAN的结构

边：可学习的1D函数矩阵
节点：求和

文档阅读

代码实操

源码阅读