1。算法细节

区间常取双闭区间，中点常向下取整，且终止条件为左区间大于右区间，且i,j都要m＋-1由于不等，保证了搜索的结束.

def binary_search(nums: list[int], target: int) -> int:
    """二分查找（双闭区间）"""
    # 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素
    i, j = 0, len(nums) - 1
    # 循环，当搜索区间为空时跳出（当 i > j 时为空）
    while i <= j:
        # 理论上 Python 的数字可以无限大（取决于内存大小），无须考虑大数越界问题
        m = (i + j) // 2  # 计算中点索引 m
        if nums[m] < target:
            i = m + 1  # 此情况说明 target 在区间 [m+1, j] 中
        elif nums[m] > target:
            j = m - 1  # 此情况说明 target 在区间 [i, m-1] 中
        else:
            return m  # 找到目标元素，返回其索引
    return -1  # 未找到目标元素，返回 -1

优点与局限性

二分查找的时间效率高。复杂度：时间O（logn），空间O（1）
二分查找仅适用于有序数据。若输入数据无序，为了使用二分查找而专门进行排序，得不偿失。因为排序算法的时间复杂度通常为O（nlogn），比线性查找和二分查找都更高。对于频繁插入元素的场景，为保持数组有序性，需要将元素插入到特定位置，时间复杂度为 O（n）。
二分查找仅适用于数组。二分查找需要跳跃式（非连续地）访问元素，而在链表中执行跳跃式访问的效率较低，因此不适合应用在链表或基于链表实现的数据结构。
小数据量下，线性查找性能更佳。

二分查找插入点（有序数组插入index问题）

问题：给定一个长度为的有序数组 nums 和一个元素 target ，数组不存在重复元素。现将 target 插入数组 nums 中，并保持其有序性。若数组中已存在元素 target ，则插入到其左方。请返回插入后 target 在数组中的索引。
解释：就是找不到时，找到应该的位置，即终止位置从return -1修改为i（终止条件为i>j，此时插入值介于区间是[i,j]，应该在i右侧，故为j）

1.不存在重复元素：找到index的位置（如果存在则是，index左侧其实就是index，Index原来的元素会后移）
2.存在重复元素：找到index最小的插入元素（当相等时，由于任务没有结束，只将右侧区间点换成j = m - 1继续搜索,其它同1.不存在重复元素.m-1不存在时会返回i=m，此时j=m-1）

寻找边界：巧

10.3 二分查找边界 - Hello 算法

一次循环判断是否存在和为某值的元素对

给定一个整数数组 nums 和一个目标元素 target ，请在数组中搜索“和”为 target 的两个元素，并返回它们的数组索引。返回任意一个解即可。
10.4 哈希优化策略 - Hello 算法
O（n）->O(1),建表只用一次

暴力搜索

线性搜索”适用于数组和链表等线性数据结构。它从数据结构的一端开始，逐个访问元素，直到找到目标元素或到达另一端仍没有找到目标元素为止。
“广度优先搜索”和“深度优先搜索”是图和树的两种遍历策略。广度优先搜索从初始节点开始逐层搜索，由近及远地访问各个节点。深度优先搜索从初始节点开始，沿着一条路径走到头，再回溯并尝试其他路径，直到遍历完整个数据结构。

自适应搜索

“二分查找”利用数据的有序性实现高效查找，仅适用于数组。
“哈希查找”利用哈希表将搜索数据和目标数据建立为键值对映射，从而实现查询操作。
“树查找”在特定的树结构（例如二叉搜索树）中，基于比较节点值来快速排除节点，从而定位目标元素。
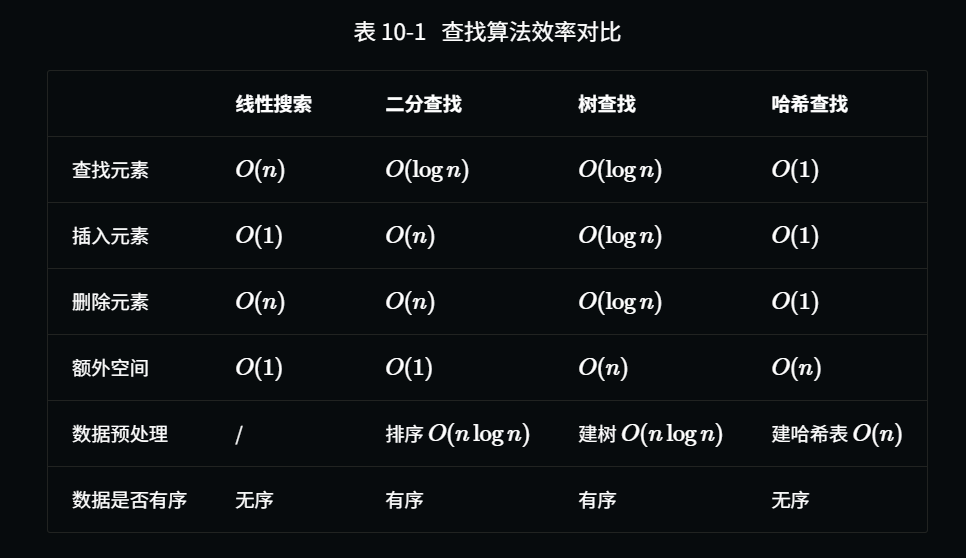
时间复杂度可达到O（logn）甚至O（1） 。

然而，使用这些算法往往需要对数据进行预处理。例如，二分查找需要预先对数组进行排序，哈希查找和树查找都需要借助额外的数据结构，维护这些数据结构也需要额外的时间和空间开销。