朴素贝叶斯算法NB

朴素贝叶斯（Naive Bayes）是一种基于贝叶斯定理的简单概率分类算法，因其高效性和良好的表现，广泛应用于文本分类、垃圾邮件过滤、情感分析等领域。尽管其”朴素”假设（特征条件独立）在现实中往往不成立，但实际效果却常常出乎意料地好。

核心思想

贝叶斯定理：
$$

P(Y|X) = \frac{P(X|Y) \cdot P(Y)}{P(X)}

(Y)：类别（如垃圾邮件/非垃圾邮件）。
(X)：特征向量（如文本中的单词）。
目标是通过已知的 (P(X|Y)) 和 (P(Y)) 计算后验概率 (P(Y|X))。

“朴素”假设：
假设所有特征在给定类别下条件独立，即：
$P(X_1, X_2, \dots, X_n|Y) = \prod_{i=1}^n P(X_i|Y)$
这使得联合概率的计算简化为各特征概率的乘积。

算法步骤

计算先验概率：

估计每个类别的概率 (P(Y))（如垃圾邮件的占比）。

计算似然概率：

对每个特征 (X_i)，计算其在每个类别下的条件概率$P(X_i|Y)$（如”免费”在垃圾邮件中出现的概率）。

预测后验概率：

对于新样本 (X = (x_1, x_2, \dots, x_n))，计算每个类别的后验概率：
$$P(Y|X) \propto P(Y) \cdot \prod_{i=1}^n P(x_i|Y)$$
选择后验概率最大的类别作为预测结果。

常见变体

最大似然估计（MLE）在朴素贝叶斯直接通过训练数据的频率统计估计参数：

先验概率 P(Y)：类别 YY 在训练集中的比例。
条件概率 P(Xi∣Y)：特征 XiXi 在类别 YY 中的出现频率。
即频率学派的默认方法：传统统计中，MLE是参数估计的经典方法，朴素贝叶斯的原始形式直接基于此。其变体是贝叶斯估计，引入参数的先验分布（如Beta分布、Dirichlet分布），通过贝叶斯定理计算后验分布：

高斯朴素贝叶斯：

适用于连续特征，假设 (P(X_i|Y)) 服从高斯分布（正态分布）。
示例：身高、体重等连续数据的分类。

多项式朴素贝叶斯：

适用于离散计数数据（如文本分类中的词频）。
使用多项式分布估计 (P(X_i|Y))。

伯努利朴素贝叶斯：

适用于二值特征（如单词是否出现）。
忽略词频，只关注”出现”或”不出现”。

拉普拉斯平滑（避免概率为0的情况，工程常用）

条件概率的贝叶斯估计为，$\lambda$=1为拉普拉斯平滑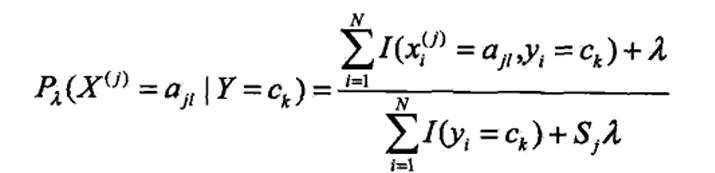

优缺点

优点：

训练和预测速度快，适合高维数据（如文本）。
对小规模数据表现良好。
对无关特征有一定鲁棒性（因独立假设）。

缺点：

特征独立性假设在现实中不成立（如”生日快乐”中的”生日”和”快乐”相关）。
需要处理零概率问题（如测试数据中出现训练中未见的特征），常用拉普拉斯平滑（加一平滑）解决：
$$P(X_i|Y) = \frac{\text{count}(X_i, Y) + \alpha}{\text{count}(Y) + \alpha \cdot n}$$
其中 $$\alpha$$是平滑参数（通常为1），$$n$$ 是特征数。

代码示例（Python）

from sklearn.naive_bayes import MultinomialNB
from sklearn.feature_extraction.text import CountVectorizer

# 示例数据：文本分类
X_train = ["free money now", "hello world", "free lottery"]
y_train = ["spam", "ham", "spam"]

# 文本向量化（词频统计）
vectorizer = CountVectorizer()
X_vec = vectorizer.fit_transform(X_train)

# 训练模型
model = MultinomialNB()
model.fit(X_vec, y_train)

# 预测新样本
X_test = ["free world"]
X_test_vec = vectorizer.transform(X_test)
print(model.predict(X_test_vec))# 输出: ['spam']

总结

朴素贝叶斯通过简化概率计算实现了高效分类，尤其适合文本和高维数据。尽管其假设较强，但在许多实际任务中表现优异，是机器学习入门和快速原型开发的经典工具。